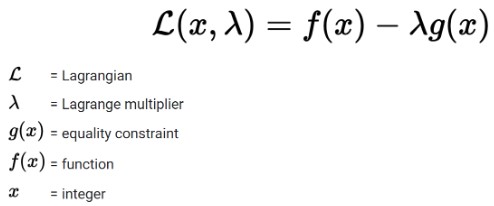Lagrange Interpolating Polynomial -- from Wolfram MathWorld

The Lagrange interpolating polynomial is the polynomial P(x) of degree <=(n-1) that passes through the n points (x_1,y_1=f(x_1)), (x_2,y_2=f(x_2)), , (x_n,y_n=f(x_n)), and is given by P(x)=sum_(j=1)^nP_j(x), (1) where P_j(x)=y_jproduct_(k=1; k!=j)^n(x-x_k)/(x_j-x_k). (2) Written explicitly, P(x) = (3) The formula was first published by Waring (1779), rediscovered by Euler in 1783, and published by Lagrange in 1795 (Jeffreys and Jeffreys 1988). Lagrange interpolating

Lagrange Interpolation Calculator - Colaboratory

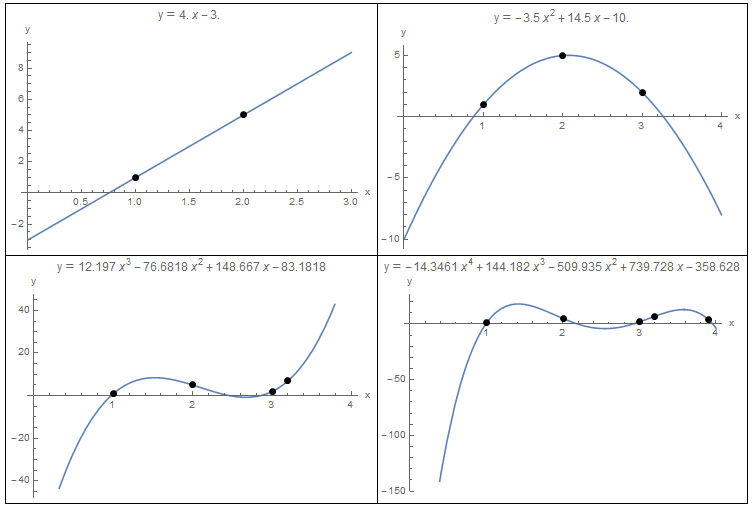
Engineering at Alberta Courses » Polynomial Interpolation

Lagrange Interpolating Polynomial -- from Wolfram MathWorld

What are the four points Lagrange interpolation polynomial that takes some value of the function (y) at the given points and estimate the value of y (10)? - Quora

Lagrange Interpolating Polynomial -- from Wolfram MathWorld

Symmetry, Free Full-Text

Hermite's Interpolating Polynomial -- from Wolfram MathWorld

Lagrange Interpolating Polynomial -- from Wolfram MathWorld

Very Number : r/mathmemes

Posts Categorized as 'Mathematics'—Wolfram

PDF) A Computational Approach for Estimating Croatia's Gini Coefficient using Lagrange Interpolation Method for Lorenz Curve Approximation

Posts Categorized as 'Mathematics'—Wolfram

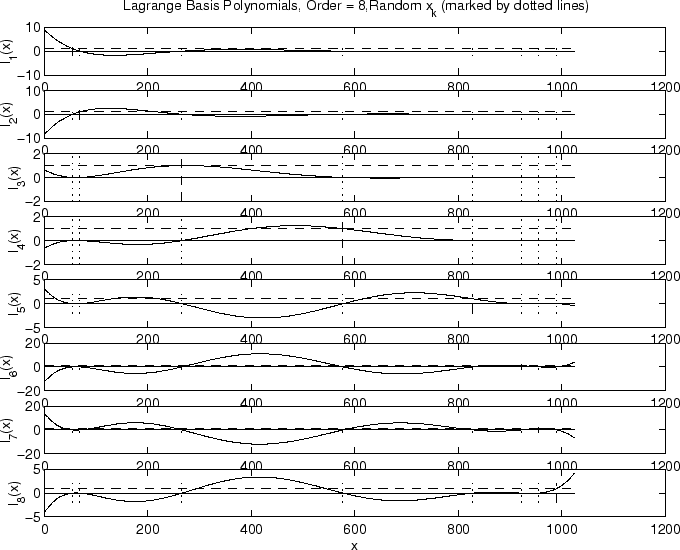
Lagrange Interpolation

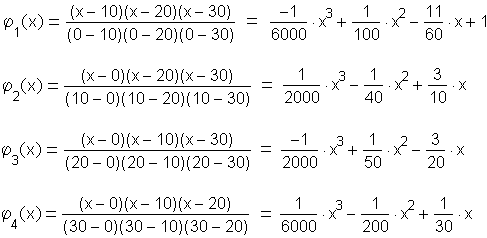
Lagrange Interpolation Polynomials

Limitations of the polynomial interpolation